Optimizers

Define the general fastai optimizer and the variants

add_docs(_BaseOptimizer, 
         all_params="List of param_groups, parameters, and hypers",
         freeze_to="Freeze parameter groups up to `n`",
         freeze="Freeze up to last parameter group",
         unfreeze="Unfreeze the entire model",
         set_hypers="`set_hyper` for all `kwargs`",
         set_hyper="Set the value(s) in `v` for hyper-parameter `k`")

---

source

Optimizer

def Optimizer(
    params:Tensor | Iterable, # Model parameters
    cbs:Callable | MutableSequence, # [`Optimizer`](https://docs.fast.ai/optimizer.html#optimizer) step callbacks
    defaults:VAR_KEYWORD
):

Base optimizer class for the fastai library, updating params with cbs

add_docs(Optimizer, 
         zero_grad="Standard PyTorch API: Zero all the grad attributes of the parameters",
         step="Standard PyTorch API: Update the stats and execute the steppers in on all parameters that have a grad",
         state_dict="Return the state of the optimizer in a dictionary",
         load_state_dict="Load the content of `sd`",
         clear_state="Reset the state of the optimizer")

Initializing an Optimizer

params will be used to create the param_groups of the optimizer. If it’s a collection (or a generator) of parameters, it will be a L containing one L with all the parameters. To define multiple parameter groups params should be passed as a collection (or a generator) of Ls.

Note

In PyTorch, model.parameters() returns a generator with all the parameters, that you can directly pass to Optimizer.

opt = Optimizer([1,2,3], noop)
test_eq(opt.param_lists, [[1,2,3]])
opt = Optimizer(range(3), noop)
test_eq(opt.param_lists, [[0,1,2]])
opt = Optimizer([[1,2],[3]], noop)
test_eq(opt.param_lists, [[1,2],[3]])
opt = Optimizer(([o,o+1] for o in range(0,4,2)), noop)
test_eq(opt.param_lists, [[0,1],[2,3]])

cbs is a list of functions that will be composed when applying the step. For instance, you can compose a function making the SGD step, with another one applying weight decay. Additionally, each cb can have a defaults attribute that contains hyper-parameters and their default value. Those are all gathered at initialization, and new values can be passed to override those defaults with the defaults kwargs. The steppers will be called by Optimizer.step (which is the standard PyTorch name), and gradients can be cleared with Optimizer.zero_grad (also a standard PyTorch name).

Once the defaults have all been pulled off, they are copied as many times as there are param_groups and stored in hypers. To apply different hyper-parameters to different groups (differential learning rates, or no weight decay for certain layers for instance), you will need to adjust those values after the init.

def tst_arg(p, lr=0, **kwargs): return p
tst_arg.defaults = dict(lr=1e-2)

def tst_arg2(p, lr2=0, **kwargs): return p
tst_arg2.defaults = dict(lr2=1e-3)

def tst_arg3(p, mom=0, **kwargs): return p
tst_arg3.defaults = dict(mom=0.9)

def tst_arg4(p, **kwargs): return p

opt = Optimizer([1,2,3], [tst_arg,tst_arg2, tst_arg3])
test_eq(opt.hypers, [{'lr2': 1e-3, 'mom': 0.9, 'lr': 1e-2}])
opt = Optimizer([1,2,3], tst_arg, lr=0.1)
test_eq(opt.hypers, [{'lr': 0.1}])
opt = Optimizer([[1,2],[3]], tst_arg)
test_eq(opt.hypers, [{'lr': 1e-2}, {'lr': 1e-2}])
opt = Optimizer([[1,2],[3]], tst_arg, lr=0.1)
test_eq(opt.hypers, [{'lr': 0.1}, {'lr': 0.1}])

For each hyper-parameter, you can pass a slice or a collection to set them, if there are multiple parameter groups. A slice will be converted to a log-uniform collection from its beginning to its end, or if it only has an end e, to a collection of as many values as there are parameter groups that are ...,e/10,e/10,e.

Setting an hyper-parameter with a collection that has a different number of elements than the optimizer has parameter groups will raise an error.

opt = Optimizer([[1,2],[3]], tst_arg, lr=[0.1,0.2])
test_eq(opt.hypers, [{'lr': 0.1}, {'lr': 0.2}])
opt = Optimizer([[1,2],[3],[4]], tst_arg, lr=slice(1e-2))
test_eq(opt.hypers, [{'lr': 1e-3}, {'lr': 1e-3}, {'lr': 1e-2}])
opt = Optimizer([[1,2],[3],[4]], tst_arg, lr=slice(1e-4,1e-2))
test_eq(opt.hypers, [{'lr': 1e-4}, {'lr': 1e-3}, {'lr': 1e-2}])
test_eq(opt.param_groups, [{'params': [1,2], 'lr': 1e-4}, {'params': [3], 'lr': 1e-3}, {'params': [4], 'lr': 1e-2}])
test_fail(lambda: Optimizer([[1,2],[3],[4]], tst_arg, lr=np.array([0.1,0.2])))

Basic steppers

To be able to give examples of optimizer steps, we will need some steppers, like the following:

---

source

sgd_step

def sgd_step(
    p, lr, kwargs:VAR_KEYWORD
):

def tst_param(val, grad=None):
    "Create a tensor with `val` and a gradient of `grad` for testing"
    res = tensor([val]).float()
    res.grad = tensor([val/10 if grad is None else grad]).float()
    return res

p = tst_param(1., 0.1)
sgd_step(p, 1.)
test_eq(p, tensor([0.9]))
test_eq(p.grad, tensor([0.1]))

---

source

weight_decay

def weight_decay(
    p, lr, wd, do_wd:bool=True, kwargs:VAR_KEYWORD
):

Weight decay as decaying p with lr*wd

p = tst_param(1., 0.1)
weight_decay(p, 1., 0.1)
test_eq(p, tensor([0.9]))
test_eq(p.grad, tensor([0.1]))

---

source

l2_reg

def l2_reg(
    p, lr, wd, do_wd:bool=True, kwargs:VAR_KEYWORD
):

L2 regularization as adding wd*p to p.grad

p = tst_param(1., 0.1)
l2_reg(p, 1., 0.1)
test_eq(p, tensor([1.]))
test_eq(p.grad, tensor([0.2]))

Warning

Weight decay and L2 regularization is the same thing for basic SGD, but for more complex optimizers, they are very different.

Making the step

---

source

Optimizer.step

def step(
    closure:NoneType=None
):

This method will loop over all param groups, then all parameters for which grad is not None and call each function in stepper, passing it the parameter p with the hyper-parameters in the corresponding dict in hypers.

#test basic step
r = L.range(4)
def tst_params(): return r.map(tst_param)

params = tst_params()
opt = Optimizer(params, sgd_step, lr=0.1)
opt.step()
test_close([p.item() for p in params], r.map(mul(0.99)))

#test two steps
params = tst_params()
opt = Optimizer(params, [weight_decay, sgd_step], lr=0.1, wd=0.1)
opt.step()
test_close([p.item() for p in params], r.map(mul(0.98)))

#test None gradients are ignored
params = tst_params()
opt = Optimizer(params, sgd_step, lr=0.1)
params[-1].grad = None
opt.step()
test_close([p.item() for p in params], [0., 0.99, 1.98, 3.])

#test discriminative lrs
params = tst_params()
opt = Optimizer([params[:2], params[2:]], sgd_step, lr=0.1)
opt.hypers[0]['lr'] = 0.01
opt.step()
test_close([p.item() for p in params], [0., 0.999, 1.98, 2.97])

---

source

Optimizer.zero_grad

def zero_grad(
    
):

params = tst_params()
opt = Optimizer(params, [weight_decay, sgd_step], lr=0.1, wd=0.1)
opt.zero_grad()
[test_eq(p.grad, tensor([0.])) for p in params];

Some of the Optimizer cbs can be functions updating the state associated with a parameter. That state can then be used by any stepper. The best example is a momentum calculation.

def tst_stat(p, **kwargs): 
    s = kwargs.get('sum', torch.zeros_like(p)) + p.data
    return {'sum': s}
tst_stat.defaults = {'mom': 0.9}

#Test Optimizer init
opt = Optimizer([1,2,3], tst_stat)
test_eq(opt.hypers, [{'mom': 0.9}])
opt = Optimizer([1,2,3], tst_stat, mom=0.99)
test_eq(opt.hypers, [{'mom': 0.99}])

#Test stat
x = torch.randn(4,5)
state = tst_stat(x)
assert 'sum' in state
test_eq(x, state['sum'])
state = tst_stat(x, **state)
test_eq(state['sum'], 2*x)

Statistics

---

source

average_grad

def average_grad(
    p, mom, dampening:bool=False, grad_avg:NoneType=None, kwargs:VAR_KEYWORD
):

Keeps track of the avg grads of p in state with mom.

dampening=False gives the classical formula for momentum in SGD:

new_val = old_val * mom + grad

whereas dampening=True makes it an exponential moving average:

new_val = old_val * mom + grad * (1-mom)

p = tst_param([1,2,3], [4,5,6])
state = {}
state = average_grad(p, mom=0.9, **state)
test_eq(state['grad_avg'], p.grad)
state = average_grad(p, mom=0.9, **state)
test_eq(state['grad_avg'], p.grad * 1.9)

#Test dampening
state = {}
state = average_grad(p,  mom=0.9, dampening=True, **state)
test_eq(state['grad_avg'], 0.1*p.grad)
state = average_grad(p, mom=0.9, dampening=True, **state)
test_close(state['grad_avg'], (0.1*0.9+0.1)*p.grad)

---

source

average_sqr_grad

def average_sqr_grad(
    p, sqr_mom, dampening:bool=True, sqr_avg:NoneType=None, kwargs:VAR_KEYWORD
):

dampening=False gives the classical formula for momentum in SGD:

new_val = old_val * mom + grad**2

whereas dampening=True makes it an exponential moving average:

new_val = old_val * mom + (grad**2) * (1-mom)

p = tst_param([1,2,3], [4,5,6])
state = {}
state = average_sqr_grad(p, sqr_mom=0.99, dampening=False, **state)
test_eq(state['sqr_avg'], p.grad.pow(2))
state = average_sqr_grad(p, sqr_mom=0.99, dampening=False, **state)
test_eq(state['sqr_avg'], p.grad.pow(2) * 1.99)

#Test dampening
state = {}
state = average_sqr_grad(p, sqr_mom=0.99, **state)
test_close(state['sqr_avg'], 0.01*p.grad.pow(2))
state = average_sqr_grad(p, sqr_mom=0.99, **state)
test_close(state['sqr_avg'], (0.01*0.99+0.01)*p.grad.pow(2))

Freezing part of the model

---

source

Optimizer.freeze

def freeze(
    
):

---

source

Optimizer.freeze_to

def freeze_to(
    n:int, # Freeze up to `n` layers
):

---

source

Optimizer.unfreeze

def unfreeze(
    
):

#Freezing the first layer
params = [tst_params(), tst_params(), tst_params()]
opt = Optimizer(params, sgd_step, lr=0.1)
opt.freeze_to(1)
req_grad = Self.requires_grad()
test_eq(L(params[0]).map(req_grad), [False]*4)
for i in {1,2}: test_eq(L(params[i]).map(req_grad), [True]*4)
    
#Unfreezing
opt.unfreeze()
for i in range(2): test_eq(L(params[i]).map(req_grad), [True]*4)

#TODO: test warning
# opt.freeze_to(3)

Parameters such as batchnorm weights/bias can be marked to always be in training mode, just put force_train=true in their state.

params = [tst_params(), tst_params(), tst_params()]
opt = Optimizer(params, sgd_step, lr=0.1)
for p in L(params[1])[[1,3]]: opt.state[p] = {'force_train': True}
opt.freeze()
test_eq(L(params[0]).map(req_grad), [False]*4)
test_eq(L(params[1]).map(req_grad), [False, True, False, True])
test_eq(L(params[2]).map(req_grad), [True]*4)

Serializing

---

source

Optimizer.state_dict

def state_dict(
    
):

---

source

Optimizer.load_state_dict

def load_state_dict(
    sd:dict, # State dict with `hypers` and `state` to load on the optimizer
):

p = tst_param([1,2,3], [4,5,6])
opt = Optimizer(p, average_grad)
opt.step()
test_eq(opt.state[p]['grad_avg'], tensor([[4., 5., 6.]]))

sd = opt.state_dict()
p1 = tst_param([10,20,30], [40,50,60])
opt = Optimizer(p1, average_grad, mom=0.99)
test_eq(opt.hypers[0]['mom'], 0.99)
test_eq(opt.state, {})

opt.load_state_dict(sd)
test_eq(opt.hypers[0]['mom'], 0.9)
test_eq(opt.state[p1]['grad_avg'], tensor([[4., 5., 6.]]))

---

source

Optimizer.clear_state

def clear_state(
    
):

p = tst_param([1,2,3], [4,5,6])
opt = Optimizer(p, average_grad)
opt.state[p] = {'force_train': True}
opt.step()
test_eq(opt.state[p]['grad_avg'], tensor([[4., 5., 6.]]))

opt.clear_state()
test_eq(opt.state[p], {'force_train': True})

Optimizers

SGD with momentum

---

source

momentum_step

def momentum_step(
    p, lr, grad_avg, kwargs:VAR_KEYWORD
):

Step for SGD with momentum with lr

---

source

SGD

def SGD(
    params:Tensor | Iterable, # Model parameters
    lr:float | slice, # Default learning rate
    mom:float=0.0, # Gradient moving average (β1) coefficient
    wd:Real=0.0, # Optional weight decay (true or L2)
    decouple_wd:bool=True, # Apply true weight decay or L2 regularization (SGD)
)->Optimizer:

A SGD Optimizer

Optional weight decay of wd is applied, as true weight decay (decay the weights directly) if decouple_wd=True else as L2 regularization (add the decay to the gradients).

#Vanilla SGD
params = tst_params()
opt = SGD(params, lr=0.1)
opt.step()
test_close([p.item() for p in params], [i*0.99 for i in range(4)])
opt.step()
test_close([p.item() for p in params], [i*0.98 for i in range(4)])

#SGD with momentum
params = tst_params()
opt = SGD(params, lr=0.1, mom=0.9)
assert isinstance(opt, Optimizer)
opt.step()
test_close([p.item() for p in params], [i*0.99 for i in range(4)])
opt.step()
test_close([p.item() for p in params], [i*(1 - 0.1 * (0.1 + 0.1*1.9)) for i in range(4)])
for i,p in enumerate(params): test_close(opt.state[p]['grad_avg'].item(), i*0.19)

Test weight decay, notice how we can see that L2 regularization is different from weight decay even for simple SGD with momentum.

params = tst_params()
#Weight decay
opt = SGD(params, lr=0.1, mom=0.9, wd=0.1)
opt.step()
test_close([p.item() for p in params], [i*0.98 for i in range(4)])
#L2 reg
opt = SGD(params, lr=0.1, mom=0.9, wd=0.1, decouple_wd=False)
opt.step()
#TODO: fix cause this formula was wrong
#test_close([p.item() for p in params], [i*0.97 for i in range(4)])

RMSProp

---

source

rms_prop_step

def rms_prop_step(
    p, lr, sqr_avg, eps, grad_avg:NoneType=None, kwargs:VAR_KEYWORD
):

Step for RMSProp with momentum with lr

---

source

RMSProp

def RMSProp(
    params:Tensor | Iterable, # Model parameters
    lr:float | slice, # Default learning rate
    mom:float=0.0, # Gradient moving average (β1) coefficient
    sqr_mom:float=0.99, # Gradient squared moving average (β2) coefficient
    eps:float=1e-08, # Added for numerical stability
    wd:Real=0.0, # Optional weight decay (true or L2)
    decouple_wd:bool=True, # Apply true weight decay or L2 regularization (RMSProp)
)->Optimizer:

A RMSProp Optimizer

RMSProp was introduced by Geoffrey Hinton in his course. What is named sqr_mom here is the alpha in the course. Optional weight decay of wd is applied, as true weight decay (decay the weights directly) if decouple_wd=True else as L2 regularization (add the decay to the gradients).

#Without momentum
params = tst_param([1,2,3], [0.1,0.2,0.3])
opt = RMSProp(params, lr=0.1)
opt.step()
test_close(params[0], tensor([0.,1.,2.]))
opt.step()
step = - 0.1 * 0.1 / (math.sqrt((0.01*0.99+0.01) * 0.1**2) + 1e-8)
test_close(params[0], tensor([step, 1+step, 2+step]))

#With momentum
params = tst_param([1,2,3], [0.1,0.2,0.3])
opt = RMSProp(params, lr=0.1, mom=0.9)
opt.step()
test_close(params[0], tensor([0.,1.,2.]))
opt.step()
step = - 0.1 * (0.1 + 0.9*0.1) / (math.sqrt((0.01*0.99+0.01) * 0.1**2) + 1e-8)
test_close(params[0], tensor([step, 1+step, 2+step]))

Adam

---

source

step_stat

def step_stat(
    p, step:int=0, kwargs:VAR_KEYWORD
):

Register the number of steps done in state for p

p = tst_param(1,0.1)
state = {}
state = step_stat(p, **state)
test_eq(state['step'], 1)
for _ in range(5): state = step_stat(p, **state)
test_eq(state['step'], 6)

---

source

debias

def debias(
    mom, damp, step
):

---

source

adam_step

def adam_step(
    p, lr, mom, step, sqr_mom, grad_avg, sqr_avg, eps, kwargs:VAR_KEYWORD
):

Step for Adam with lr on p

---

source

Adam

def Adam(
    params:Tensor | Iterable, # Model parameters
    lr:float | slice, # Default learning rate
    mom:float=0.9, # Gradient moving average (β1) coefficient
    sqr_mom:float=0.99, # Gradient squared moving average (β2) coefficient
    eps:float=1e-05, # Added for numerical stability
    wd:Real=0.01, # Optional weight decay (true or L2)
    decouple_wd:bool=True, # Apply true weight decay (AdamW) or L2 regularization (Adam)
)->Optimizer:

A Adam/AdamW Optimizer

Adam was introduced by Diederik P. Kingma and Jimmy Ba in Adam: A Method for Stochastic Optimization. For consistency across optimizers, we renamed beta1 and beta2 in the paper to mom and sqr_mom. Note that our defaults also differ from the paper (0.99 for sqr_mom or beta2, 1e-5 for eps). Those values seem to be better from our experiments in a wide range of situations.

Optional weight decay of wd is applied, as true weight decay (decay the weights directly) if decouple_wd=True else as L2 regularization (add the decay to the gradients).

Note

Don’t forget that eps is an hyper-parameter you can change. Some models won’t train without a very high eps like 0.1 (intuitively, the higher eps is, the closer we are to normal SGD). The usual default of 1e-8 is often too extreme in the sense we don’t manage to get as good results as with SGD.

params = tst_param([1,2,3], [0.1,0.2,0.3])
opt = Adam(params, lr=0.1, wd=0)
opt.step()
step = -0.1 * 0.1 / (math.sqrt(0.1**2) + 1e-8)
test_close(params[0], tensor([1+step, 2+step, 3+step]))
opt.step()
test_close(params[0], tensor([1+2*step, 2+2*step, 3+2*step]), eps=1e-3)

RAdam

RAdam (for rectified Adam) was introduced by Zhang et al. in On the Variance of the Adaptive Learning Rate and Beyond to slightly modify the Adam optimizer to be more stable at the beginning of training (and thus not require a long warmup). They use an estimate of the variance of the moving average of the squared gradients (the term in the denominator of traditional Adam) and rescale this moving average by this term before performing the update.

This version also incorporates SAdam; set beta to enable this (definition same as in the paper).

---

source

radam_step

def radam_step(
    p, lr, mom, step, sqr_mom, grad_avg, sqr_avg, eps, beta, kwargs:VAR_KEYWORD
):

Step for RAdam with lr on p

---

source

RAdam

def RAdam(
    params:Tensor | Iterable, # Model parameters
    lr:float | slice, # Default learning rate
    mom:float=0.9, # Gradient moving average (β1) coefficient
    sqr_mom:float=0.99, # Gradient squared moving average (β2) coefficient
    eps:float=1e-05, # Added for numerical stability
    wd:Real=0.0, # Optional weight decay (true or L2)
    beta:float=0.0, # Set to enable SAdam
    decouple_wd:bool=True, # Apply true weight decay (RAdamW) or L2 regularization (RAdam)
)->Optimizer:

A RAdam/RAdamW Optimizer

This is the effective correction reported to the adam step for 500 iterations in RAdam. We can see how it goes from 0 to 1, mimicking the effect of a warm-up.

beta = 0.99
r_inf = 2/(1-beta) - 1
rs = np.array([r_inf - 2*s*beta**s/(1-beta**s) for s in range(5,500)])
v = np.sqrt(((rs-4) * (rs-2) * r_inf)/((r_inf-4)*(r_inf-2)*rs))
plt.plot(v);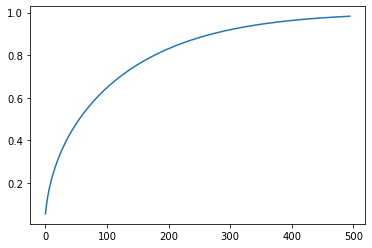

params = tst_param([1,2,3], [0.1,0.2,0.3])
opt = RAdam(params, lr=0.1)
#The r factor is lower than 5 during the first 5 steps so updates use the average of gradients (all the same)
r_inf = 2/(1-0.99) - 1
for i in range(5): 
    r = r_inf - 2*(i+1)*0.99**(i+1)/(1-0.99**(i+1))
    assert r <= 5
    opt.step()
p = tensor([0.95, 1.9, 2.85])
test_close(params[0], p)

#The r factor is greater than 5 for the sixth step so we update with RAdam
r = r_inf - 2*6*0.99**6/(1-0.99**6)
assert r > 5
opt.step()
v = math.sqrt(((r-4) * (r-2) * r_inf)/((r_inf-4)*(r_inf-2)*r))
step = -0.1*0.1*v/(math.sqrt(0.1**2) + 1e-8)
test_close(params[0], p+step)

QHAdam

QHAdam (for Quasi-Hyperbolic Adam) was introduced by Ma & Yarats in Quasi-Hyperbolic Momentum and Adam for Deep Learning as a “computationally cheap, intuitive to interpret, and simple to implement” optimizer. Additional code can be found in their qhoptim repo. QHAdam is based on QH-Momentum, which introduces the immediate discount factor nu, encapsulating plain SGD (nu = 0) and momentum (nu = 1). QH-Momentum is defined below, where g_t+1 is the update of the moment. An interpretation of QHM is as a nu-weighted average of the momentum update step and the plain SGD update step.

θ_t+1 ← θ_t − lr * [(1 − nu) · ∇L_t(θ_t) + nu · g_t+1]

QHAdam takes the concept behind QHM above and applies it to Adam, replacing both of Adam’s moment estimators with quasi-hyperbolic terms.

The paper’s suggested default parameters are mom = 0.999, sqr_mom = 0.999, nu_1 = 0.7 and and nu_2 = 1.0. When training is not stable, it is possible that setting nu_2 < 1 can improve stability by imposing a tighter step size bound. Note that QHAdam recovers Adam when nu_1 = nu_2 = 1.0. QHAdam recovers RMSProp (Hinton et al., 2012) when nu_1 = 0 and nu_2 = 1, and NAdam (Dozat, 2016) when nu_1 = mom and nu_2 = 1.

Optional weight decay of wd is applied, as true weight decay (decay the weights directly) if decouple_wd=True else as L2 regularization (add the decay to the gradients).

---

source

qhadam_step

def qhadam_step(
    p, lr, mom, sqr_mom, sqr_avg, nu_1, nu_2, step, grad_avg, eps, kwargs:VAR_KEYWORD
):

---

source

QHAdam

def QHAdam(
    params:Tensor | Iterable, # Model parameters
    lr:float | slice, # Default learning rate
    mom:float=0.999, # Gradient moving average (β1) coefficient
    sqr_mom:float=0.999, # Gradient squared moving average (β2) coefficient
    nu_1:float=0.7, # QH immediate discount factor
    nu_2:float=1.0, # QH momentum discount factor
    eps:float=1e-08, # Added for numerical stability
    wd:Real=0.0, # Optional weight decay (true or L2)
    decouple_wd:bool=True, # Apply true weight decay (QHAdamW) or L2 regularization (QHAdam)
)->Optimizer:

A QHAdam/QHAdamW Optimizer

params = tst_param([1,2,3], [0.1,0.2,0.3])
opt = QHAdam(params, lr=0.1)
opt.step()
step = -0.1 * (((1-0.7) * 0.1) + (0.7 * 0.1)) / (
     math.sqrt(((1-1.0) * 0.1**2) + (1.0 * 0.1**2)) + 1e-8) 
test_close(params[0], tensor([1+step, 2+step, 3+step]))
opt.step()
test_close(params[0], tensor([1+2*step, 2+2*step, 3+2*step]), eps=1e-3)

LARS/LARC

---

source

larc_layer_lr

def larc_layer_lr(
    p, lr, trust_coeff, wd, eps, clip:bool=True, kwargs:VAR_KEYWORD
):

Computes the local lr before weight decay is applied

---

source

larc_step

def larc_step(
    p, local_lr, grad_avg:NoneType=None, kwargs:VAR_KEYWORD
):

Step for LARC local_lr on p

---

source

Larc

def Larc(
    params:Tensor | Iterable, # Model parameters
    lr:float | slice, # Default learning rate
    mom:float=0.9, # Gradient moving average (β1) coefficient
    clip:bool=True, # LARC if clip=True, LARS if clip=False
    trust_coeff:float=0.02, # Trust coeffiecnet for calculating layerwise LR
    eps:float=1e-08, # Added for numerical stability
    wd:Real=0.0, # Optional weight decay (true or L2)
    decouple_wd:bool=True, # Apply true weight decay or L2 regularization
)->Optimizer:

A LARC/LARS Optimizer

The LARS optimizer was first introduced in Large Batch Training of Convolutional Networks then refined in its LARC variant (original LARS is with clip=False). A learning rate is computed for each individual layer with a certain trust_coefficient, then clipped to be always less than lr.

Optional weight decay of wd is applied, as true weight decay (decay the weights directly) if decouple_wd=True else as L2 regularization (add the decay to the gradients).

params = [tst_param([1,2,3], [0.1,0.2,0.3]), tst_param([1,2,3], [0.01,0.02,0.03])]
opt = Larc(params, lr=0.1)
opt.step()
#First param local lr is 0.02 < lr so it's not clipped
test_close(opt.state[params[0]]['local_lr'], 0.02)
#Second param local lr is 0.2 > lr so it's clipped
test_eq(opt.state[params[1]]['local_lr'], 0.1)
test_close(params[0], tensor([0.998,1.996,2.994]))
test_close(params[1], tensor([0.999,1.998,2.997]))

params = [tst_param([1,2,3], [0.1,0.2,0.3]), tst_param([1,2,3], [0.01,0.02,0.03])]
opt = Larc(params, lr=0.1, clip=False)
opt.step()
#No clipping
test_close(opt.state[params[0]]['local_lr'], 0.02)
test_close(opt.state[params[1]]['local_lr'], 0.2)
test_close(params[0], tensor([0.998,1.996,2.994]))
test_close(params[1], tensor([0.998,1.996,2.994]))

LAMB

---

source

lamb_step

def lamb_step(
    p, lr, mom, step, sqr_mom, grad_avg, sqr_avg, eps, kwargs:VAR_KEYWORD
):

Step for LAMB with lr on p

---

source

Lamb

def Lamb(
    params:Tensor | Iterable, # Model parameters
    lr:float | slice, # Default learning rate
    mom:float=0.9, # Gradient moving average (β1) coefficient
    sqr_mom:float=0.99, # Gradient squared moving average (β2) coefficient
    eps:float=1e-05, # Added for numerical stability
    wd:Real=0.0, # Optional weight decay (true or L2)
    decouple_wd:bool=True, # Apply true weight decay or L2 regularization
)->Optimizer:

A LAMB Optimizer

LAMB was introduced in Large Batch Optimization for Deep Learning: Training BERT in 76 minutes. Intuitively, it’s LARC applied to Adam. As in Adam, we renamed beta1 and beta2 in the paper to mom and sqr_mom. Note that our defaults also differ from the paper (0.99 for sqr_mom or beta2, 1e-5 for eps). Those values seem to be better from our experiments in a wide range of situations.

Optional weight decay of wd is applied, as true weight decay (decay the weights directly) if decouple_wd=True else as L2 regularization (add the decay to the gradients).

params = tst_param([1,2,3], [0.1,0.2,0.3])
opt = Lamb(params, lr=0.1)
opt.step()
test_close(params[0], tensor([0.7840,1.7840,2.7840]), eps=1e-3)

Lookahead was introduced by Zhang et al. in Lookahead Optimizer: k steps forward, 1 step back. It can be run on top of any optimizer and consists in having the final weights of the model be a moving average. In practice, we update our model using the internal optimizer but keep a copy of old weights that and every k steps, we change the weights by a moving average of the fast weights (the ones updated by the inner optimizer) with the slow weights (the copy of old weights). Those slow weights act like a stability mechanism.

---

source

Lookahead

def Lookahead(
    opt:Optimizer, # [`Optimizer`](https://docs.fast.ai/optimizer.html#optimizer) to wrap with Lookahead
    k:int=6, # How often to conduct Lookahead step
    alpha:float=0.5, # Slow weight moving average coefficient
):

Wrap opt in a lookahead optimizer

params = tst_param([1,2,3], [0.1,0.2,0.3])
p,g = params[0].data.clone(),tensor([0.1,0.2,0.3])
opt = Lookahead(SGD(params, lr=0.1))
for k in range(5): opt.step()
#first 5 steps are normal SGD steps
test_close(params[0], p - 0.5*g)
#Since k=6, sixth step is a moving average of the 6 SGD steps with the initial weight
opt.step()
test_close(params[0], p * 0.5 + (p-0.6*g) * 0.5)

---

source

ranger

def ranger(
    params:Tensor | Iterable, # Model parameters
    lr:float | slice, # Default learning rate
    mom:float=0.95, # Gradient moving average (β1) coefficient
    wd:Real=0.01, # Optional weight decay (true or L2)
    eps:float=1e-06, # Added for numerical stability
    k:int=6, # How often to conduct Lookahead step
    alpha:float=0.5, # Slow weight moving average coefficient
    sqr_mom:float=0.99, # Gradient squared moving average (β2) coefficient
    beta:float=0.0, # Set to enable SAdam
    decouple_wd:bool=True, # Apply true weight decay (RAdamW) or L2 regularization (RAdam)
)->Lookahead:

Convenience method for Lookahead with RAdam

OptimWrapper provides simple functionality to use existing optimizers constructed with torch.optim.Optimizer.

---

source

detuplify_pg

def detuplify_pg(
    d
):

---

source

set_item_pg

def set_item_pg(
    pg, k, v
):

---

source

OptimWrapper

def OptimWrapper(
    params:Tensor | Iterable=None, # Model parameters. Don't set if using a built optimizer
    opt:Callable | torch.optim.Optimizer=None, # A torch optimizer constructor, or an already built optimizer
    hp_map:dict=None, # A dictionary converting PyTorch optimizer keys to fastai's [`Optimizer`](https://docs.fast.ai/optimizer.html#optimizer) keys. Defaults to `pytorch_hp_map`
    convert_groups:bool=True, # Convert parameter groups from splitter or pass unaltered to `opt`
    kwargs:VAR_KEYWORD
):

A wrapper class for existing PyTorch optimizers

To use an existing PyTorch optimizer, you can define an optimizer function like this:

opt_func = partial(OptimWrapper, opt=torch.optim.SGD)

Or if you already have a built optimizer, pass in only opt:

opt = torch.optim.SGD([tensor([1,2,3])], lr=1e-2)
opt_func = OptimWrapper(opt=opt)

When passing a built optimizer to Learner, instead of resetting the optimizer Learner.fit will clear the optimizer state if reset_opt=True or when calling Learner.fit for the first time.

To prevent Learner from clearing the optimizer state when calling Learner.fit for the first time, assign the optimizer directly to Learner.opt:

opt = torch.optim.SGD([tensor([1,2,3])], lr=1e-2)
learn = Learner(..., opt_func=None)
learn.opt = OptimWrapper(opt=opt)