from fastai.test_utils import *Hyperparam schedule
Annealing
annealer
annealer (f)
Decorator to make f return itself partially applied.
This is the decorator we will use for all of our scheduling functions, as it transforms a function taking (start, end, pos) to something taking (start, end) and return a function depending of pos.
sched_exp
sched_exp (start, end, pos)
sched_no
sched_no (start, end, pos)
sched_cos
sched_cos (start, end, pos)
sched_lin
sched_lin (start, end, pos)
annealings = "NO LINEAR COS EXP".split()
p = torch.linspace(0.,1,100)
fns = [SchedNo, SchedLin, SchedCos, SchedExp]for fn, t in zip(fns, annealings):
plt.plot(p, [fn(2, 1e-2)(o) for o in p], label=t)
f = SchedPoly(2,1e-2,0.5)
plt.plot(p, [f(o) for o in p], label="POLY(0.5)")
plt.legend();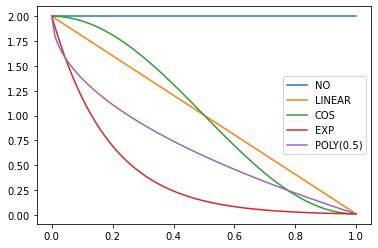
SchedLin
SchedLin (start, end)
Linear schedule function from start to end
sched = SchedLin(0, 2)
test_eq(L(map(sched, [0., 0.25, 0.5, 0.75, 1.])), [0., 0.5, 1., 1.5, 2.])SchedCos
SchedCos (start, end)
Cosine schedule function from start to end
sched = SchedCos(0, 2)
test_close(L(map(sched, [0., 0.25, 0.5, 0.75, 1.])), [0., 0.29289, 1., 1.70711, 2.])SchedNo
SchedNo (start, end)
Constant schedule function with start value
sched = SchedNo(0, 2)
test_close(L(map(sched, [0., 0.25, 0.5, 0.75, 1.])), [0., 0., 0., 0., 0.])SchedExp
SchedExp (start, end)
Exponential schedule function from start to end
sched = SchedExp(1, 2)
test_close(L(map(sched, [0., 0.25, 0.5, 0.75, 1.])), [1., 1.18921, 1.41421, 1.68179, 2.])SchedPoly
SchedPoly (start, end, power)
Polynomial schedule (of power) function from start to end
sched = SchedPoly(0, 2, 2)
test_close(L(map(sched, [0., 0.25, 0.5, 0.75, 1.])), [0., 0.125, 0.5, 1.125, 2.])p = torch.linspace(0.,1,100)
pows = [0.5,1.,2.]
for e in pows:
f = SchedPoly(2, 0, e)
plt.plot(p, [f(o) for o in p], label=f'power {e}')
plt.legend();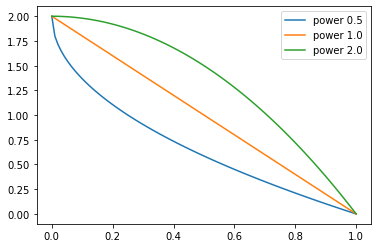
combine_scheds
combine_scheds (pcts, scheds)
Combine scheds according to pcts in one function
pcts must be a list of positive numbers that add up to 1 and is the same length as scheds. The generated function will use scheds[0] from 0 to pcts[0] then scheds[1] from pcts[0] to pcts[0]+pcts[1] and so forth.
p = torch.linspace(0.,1,100)
f = combine_scheds([0.3,0.7], [SchedCos(0.3,0.6), SchedCos(0.6,0.2)])
plt.plot(p, [f(o) for o in p]);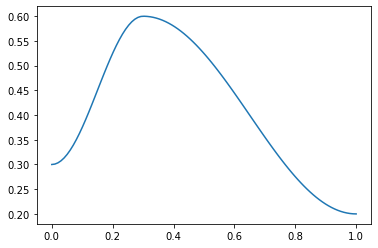
p = torch.linspace(0.,1,100)
f = combine_scheds([0.3,0.2,0.5], [SchedLin(0.,1.), SchedNo(1.,1.), SchedCos(1., 0.)])
plt.plot(p, [f(o) for o in p]);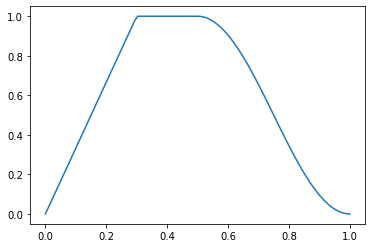
combined_cos
combined_cos (pct, start, middle, end)
Return a scheduler with cosine annealing from start→middle & middle→end
This is a useful helper function for the 1cycle policy. pct is used for the start to middle part, 1-pct for the middle to end. Handles floats or collection of floats. For example:
f = combined_cos(0.25,0.5,1.,0.)
plt.plot(p, [f(o) for o in p]);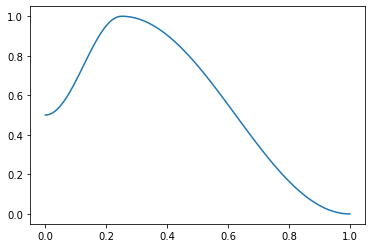
ParamScheduler
ParamScheduler (scheds)
Schedule hyper-parameters according to scheds
scheds is a dictionary with one key for each hyper-parameter you want to schedule, with either a scheduler or a list of schedulers as values (in the second case, the list must have the same length as the the number of parameters groups of the optimizer).
learn = synth_learner()
sched = {'lr': SchedLin(1e-3, 1e-2)}
learn.fit(1, cbs=ParamScheduler(sched))
n = len(learn.dls.train)
test_close(learn.recorder.hps['lr'], [1e-3 + (1e-2-1e-3) * i/n for i in range(n)])| epoch | train_loss | valid_loss | time |
|---|---|---|---|
| 0 | 11.929138 | 4.039281 | 00:00 |
ParamScheduler.before_fit
ParamScheduler.before_fit ()
Initialize container for hyper-parameters
ParamScheduler.before_batch
ParamScheduler.before_batch ()
Set the proper hyper-parameters in the optimizer
ParamScheduler.after_batch
ParamScheduler.after_batch ()
Record hyper-parameters of this batch
ParamScheduler.after_fit
ParamScheduler.after_fit ()
Save the hyper-parameters in the recorder if there is one
Learner.fit_one_cycle
Learner.fit_one_cycle (n_epoch, lr_max=None, div=25.0, div_final=100000.0, pct_start=0.25, wd=None, moms=None, cbs=None, reset_opt=False, start_epoch=0)
Fit self.model for n_epoch using the 1cycle policy.
The 1cycle policy was introduced by Leslie N. Smith et al. in Super-Convergence: Very Fast Training of Neural Networks Using Large Learning Rates. It schedules the learning rate with a cosine annealing from lr_max/div to lr_max then lr_max/div_final (pass an array to lr_max if you want to use differential learning rates) and the momentum with cosine annealing according to the values in moms. The first phase takes pct_start of the training. You can optionally pass additional cbs and reset_opt.
#Integration test: training a few epochs should make the model better
learn = synth_learner(lr=1e-2)
xb,yb = learn.dls.one_batch()
init_loss = learn.loss_func(learn.model(xb), yb)
learn.fit_one_cycle(2)
xb,yb = learn.dls.one_batch()
final_loss = learn.loss_func(learn.model(xb), yb)
assert final_loss < init_loss| epoch | train_loss | valid_loss | time |
|---|---|---|---|
| 0 | 19.444899 | 6.755066 | 00:00 |
| 1 | 9.919473 | 1.044571 | 00:00 |
#Scheduler test
lrs,moms = learn.recorder.hps['lr'],learn.recorder.hps['mom']
test_close(lrs, [combined_cos(0.25,1e-2/25,1e-2,1e-7)(i/20) for i in range(20)])
test_close(moms, [combined_cos(0.25,0.95,0.85,0.95)(i/20) for i in range(20)])Recorder.plot_sched
Recorder.plot_sched (keys=None, figsize=None)
learn = synth_learner()
learn.fit_one_cycle(2)| epoch | train_loss | valid_loss | time |
|---|---|---|---|
| 0 | 5.406837 | 5.305011 | 00:00 |
| 1 | 5.058437 | 4.899223 | 00:00 |
learn.recorder.plot_sched()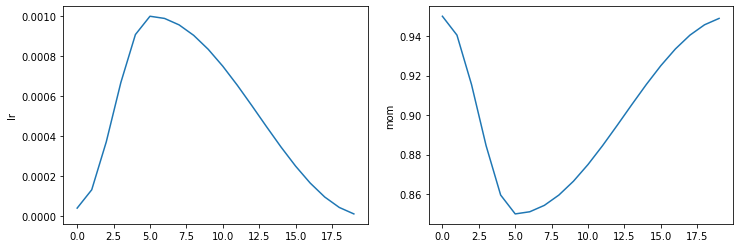
Learner.fit_flat_cos
Learner.fit_flat_cos (n_epoch, lr=None, div_final=100000.0, pct_start=0.75, wd=None, cbs=None, reset_opt=False, start_epoch=0)
Fit self.model for n_epoch at flat lr before a cosine annealing.
learn = synth_learner()
learn.fit_flat_cos(2)| epoch | train_loss | valid_loss | time |
|---|---|---|---|
| 0 | 10.588930 | 7.106113 | 00:00 |
| 1 | 8.943380 | 5.016665 | 00:00 |
learn.recorder.plot_sched()
Learner.fit_sgdr
Learner.fit_sgdr (n_cycles, cycle_len, lr_max=None, cycle_mult=2, cbs=None, reset_opt=False, wd=None, start_epoch=0)
Fit self.model for n_cycles of cycle_len using SGDR.
This schedule was introduced by Ilya Loshchilov et al. in SGDR: Stochastic Gradient Descent with Warm Restarts. It consists of n_cycles that are cosine annealings from lr_max (defaults to the Learner lr) to 0, with a length of cycle_len * cycle_mult**i for the i-th cycle (first one is cycle_len-long, then we multiply the length by cycle_mult at each epoch). You can optionally pass additional cbs and reset_opt.
learn = synth_learner()
with learn.no_logging(): learn.fit_sgdr(3, 1)
test_eq(learn.n_epoch, 7)
iters = [k * len(learn.dls.train) for k in [0,1,3,7]]
for i in range(3):
n = iters[i+1]-iters[i]
#The start of a cycle can be mixed with the 0 of the previous cycle with rounding errors, so we test at +1
test_close(learn.recorder.lrs[iters[i]+1:iters[i+1]], [SchedCos(learn.lr, 0)(k/n) for k in range(1,n)])
learn.recorder.plot_sched()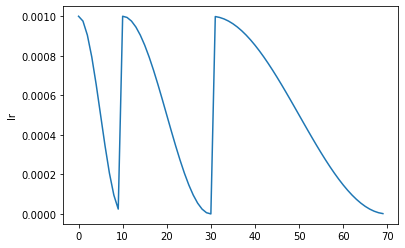
Learner.fine_tune
Learner.fine_tune (epochs, base_lr=0.002, freeze_epochs=1, lr_mult=100, pct_start=0.3, div=5.0, lr_max=None, div_final=100000.0, wd=None, moms=None, cbs=None, reset_opt=False, start_epoch=0)
Fine tune with Learner.freeze for freeze_epochs, then with Learner.unfreeze for epochs, using discriminative LR.
learn.fine_tune(1)| epoch | train_loss | valid_loss | time |
|---|---|---|---|
| 0 | 2.428970 | 1.740237 | 00:00 |
| epoch | train_loss | valid_loss | time |
|---|---|---|---|
| 0 | 2.019952 | 1.616970 | 00:00 |
Resume training from checkpoint
To enable resuming from checkpoint make sure to save model and optimizer state. This can be done using SaveModelCallback setting (with_opt=True). If training is interrupted define learn using the same parameters as before, load model from checkpoint and pass start_epoch to fit call. The training will be resumed from start_epoch with properly scheduled lr.
with tempfile.TemporaryDirectory() as d:
learn1 = synth_learner(path=d, cbs=SaveModelCallback(with_opt=True, fname="ckpt"))
learn1.fit_one_cycle(5, cbs=InterruptCallback(2))
learn2 = synth_learner(path=d)
learn2 = learn2.load("ckpt")
learn2.fit_one_cycle(5, start_epoch=2)
fig, axs = plt.subplots(1,2, sharey=True)
axs[0].plot(learn1.recorder.lrs)
axs[1].plot(learn2.recorder.lrs)| epoch | train_loss | valid_loss | time |
|---|---|---|---|
| 0 | 18.930223 | 14.100439 | 00:00 |
| 1 | 17.092665 | 10.603369 | 00:00 |
Better model found at epoch 0 with valid_loss value: 14.100439071655273.
Better model found at epoch 1 with valid_loss value: 10.603368759155273.| epoch | train_loss | valid_loss | time |
|---|---|---|---|
| 0 | 00:00 | ||
| 1 | 00:00 | ||
| 2 | 11.456764 | 10.057186 | 00:00 |
| 3 | 10.287196 | 8.694046 | 00:00 |
| 4 | 9.585465 | 8.422710 | 00:00 |
LRFinder
LRFinder (start_lr=1e-07, end_lr=10, num_it=100, stop_div=True)
Training with exponentially growing learning rate
from fastai.vision.all import *set_seed(99, True)
path = untar_data(URLs.PETS)/'images'
image_files = get_image_files(path)
if sys.platform == "win32" and IN_NOTEBOOK:
image_files = random.choices(image_files, k=int(len(image_files)/8))
print("Randomly select 1/8 files in NOTEBOOK on Windows to save time")
# pickle can't serializer lamda function.
def _label_func(x):
return x[0].isupper()
dls = ImageDataLoaders.from_name_func(
path, image_files, valid_pct=0.2,
label_func=_label_func, item_tfms=Resize(224))
learn = vision_learner(dls, resnet18)
learn.fit(1)
learn.opt.state_dict()['state'][1]['grad_avg']| epoch | train_loss | valid_loss | time |
|---|---|---|---|
| 0 | 0.086690 | 0.016682 | 00:33 |
tensor([-5.8191e-04, -2.2443e-03, 0.0000e+00, -1.2517e-03, 0.0000e+00,
-1.4744e-03, -3.6433e-04, 0.0000e+00, 9.3745e-03, 0.0000e+00,
5.1993e-03, -1.5093e-02, -4.0410e-03, 0.0000e+00, 7.1963e-03,
-6.6033e-03, -3.3354e-03, -2.9191e-03, -1.5054e-03, -1.3179e-03,
8.7333e-03, -1.1155e-02, -9.6656e-04, 1.6653e-02, 9.5839e-04,
8.4995e-03, -2.8187e-02, 3.1579e-03, -9.3051e-04, -2.3887e-03,
-7.3557e-04, -1.4501e-02, -6.2110e-03, 1.9949e-03, -7.0233e-03,
1.2792e-02, 0.0000e+00, 1.0687e-03, 0.0000e+00, -4.2413e-04,
2.9628e-03, 7.2686e-03, -9.7241e-03, -4.9941e-04, 1.7408e-02,
-9.2441e-03, -9.7731e-03, -9.9393e-03, 0.0000e+00, -2.1448e-03,
2.7660e-03, -3.1110e-03, 5.9454e-05, -1.4412e-03, -6.1454e-04,
-1.6537e-03, 1.7001e-02, 1.4041e-02, -6.2878e-03, 2.0800e-02,
-1.2900e-02, -1.2626e-02, -2.6591e-03, 3.9685e-03], device='cuda:0')with tempfile.TemporaryDirectory() as d:
learn = synth_learner(path=Path(d))
init_a,init_b = learn.model.a,learn.model.b
with learn.no_logging(): learn.fit(20, cbs=LRFinder(num_it=100))
assert len(learn.recorder.lrs) <= 100
test_eq(len(learn.recorder.lrs), len(learn.recorder.losses))
#Check stop if diverge
if len(learn.recorder.lrs) < 100: assert learn.recorder.losses[-1] > 4 * min(learn.recorder.losses)
#Test schedule
test_eq(learn.recorder.lrs, [SchedExp(1e-7, 10)(i/100) for i in range_of(learn.recorder.lrs)])
#No validation data
test_eq([len(v) for v in learn.recorder.values], [1 for _ in range_of(learn.recorder.values)])
#Model loaded back properly
test_eq(learn.model.a, init_a)
test_eq(learn.model.b, init_b)
test_eq(learn.opt.state_dict()['state'], [{}, {}])LRFinder.before_fit
LRFinder.before_fit ()
Initialize container for hyper-parameters and save the model
LRFinder.before_batch
LRFinder.before_batch ()
Set the proper hyper-parameters in the optimizer
LRFinder.after_batch
LRFinder.after_batch ()
Record hyper-parameters of this batch and potentially stop training
LRFinder.before_validate
LRFinder.before_validate ()
Skip the validation part of training
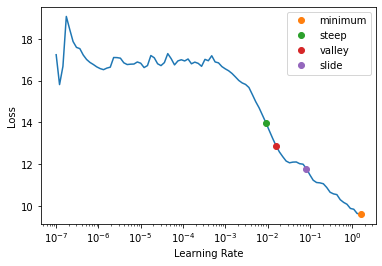
Suggestion Methods
There are a few methodologies for suggesting a learning rate automatically and these as we will see can further be passed into lr_find. Currently four methods are supported, however to write your own it should look like a function that can accept LRFinder’s returned lrs, losses, as well as the num_it. Your function should return an x,y coordinate that can be plotted, such as below:
def myfunc(lrs:list, losses:list, num_it:int) -> tuple(float, tuple(float,int)):
...
return suggestion, (suggestion,loss_idx)If there are any more parameters to be passed in, you should pass in your func as a partial and specify them yourself, such as:
def myfunc(lrs:list, losses:list, num_it:int, pct_reduction:float) -> tuple(float, tuple(float,int)):
...
return suggestion, (suggestion,loss_idx)f = partial(myfunc, pct_reduction=.2)valley
valley (lrs:list, losses:list, num_it:int)
Suggests a learning rate from the longest valley and returns its index
The valley algorithm was developed by ESRI and takes the steepest slope roughly 2/3 through the longest valley in the LR plot, and is also the default for Learner.lr_find
slide
slide (lrs:list, losses:list, num_it:int, lr_diff:int=15, thresh:float=0.005, adjust_value:float=1.0)
Suggests a learning rate following an interval slide rule and returns its index
The slide rule is an algorithm developed by Andrew Chang out of Novetta, and is detailed here.
minimum
minimum (lrs:list, losses:list, num_it:int)
Suggests a learning rate one-tenth the minumum before divergance and returns its index
steep
steep (lrs:list, losses:list, num_it:int)
Suggests a learning rate when the slope is the steepest and returns its index
Recorder.plot_lr_find
Recorder.plot_lr_find (skip_end=5, return_fig=True, suggestions=None, nms=None, **kwargs)
Plot the result of an LR Finder test (won’t work if you didn’t do learn.lr_find() before)
Learner.lr_find
Learner.lr_find (start_lr=1e-07, end_lr=10, num_it=100, stop_div=True, show_plot=True, suggest_funcs=<function valley>)
Launch a mock training to find a good learning rate and return suggestions based on suggest_funcs as a named tuple
First introduced by Leslie N. Smith in Cyclical Learning Rates for Training Neural Networks, the LR Finder trains the model with exponentially growing learning rates from start_lr to end_lr for num_it and stops in case of divergence (unless stop_div=False) then plots the losses vs the learning rates with a log scale.
A variety of learning rate suggestion algorithms can be passed into the function, by default we use the valley paradigm.
with tempfile.TemporaryDirectory() as d:
learn = synth_learner(path=Path(d))
weights_pre_lr_find = L(learn.model.parameters())
lr_min, lr_steep, lr_valley, lr_slide = learn.lr_find(suggest_funcs=(minimum, steep, valley, slide))
weights_post_lr_find = L(learn.model.parameters())
test_eq(weights_pre_lr_find, weights_post_lr_find)
print(f"Minimum/10:\t{lr_min:.2e}\nSteepest point:\t{lr_steep:.2e}\nLongest valley:\t{lr_valley:.2e}\nSlide interval:\t{lr_slide:.2e}")Minimum/10: 1.58e-01
Steepest point: 9.12e-03
Longest valley: 1.58e-02
Slide interval: 8.32e-02